[백준] (2981) 검문
링크 : https://www.acmicpc.net/problem/2981
사용 언어 : JAVA
내 생각
대체 왜 그랬는지는 모르겠는데 골드 4라 쉽겠지 생각했다. 근데 아무리 생각해도 어떻게 해야하는지 감도 안오고,, 혹시나 제출해봐도 계속 틀리고 시간초과나고ㅋㅋㅋ 결국 멘탈 터져서 나중에는 출력에 println 써서 0퍼 컷 당하고 그랬다ㅎㅎ;; 처음에 쉽다고 얕봐서 더 멘탈이 나간 듯 하다.
결국 패배를 인정하고 구글링했다. 그리고 내 기초 지식이 부실했음을 깨닫고 컴공의 기본 of 기본인 유클리드 호제에 대해 다시 공부하였고, 까먹지 않기 위해 울면서 포스팅을 쓴다 ㅠㅠ
초기 생각
사실 맨 처음에도 유클리드 호제 같긴 했는데 당최 어떻게 써먹어야하는질 몰라서 그냥 냅다 풀었다.
for (extra = 1~MIN) {
gcd = (i=0~N)(arr[i] - extra)들의 최대공약수
pq.add(gcd 약수)
}딱봐도 시간 초과나게 생김
최종
유클리드 호제법에 대한 포스팅은 여기에 따로 적어두었다.
일단 이 문제는 주어진 숫자들의 나머지를 같게 만드는 나누는 수 M을 찾는 것이 목적이다. M은 반드시 하나 이상 존재한다고 문제에 나와 있으니, 주어진 수 A, B, C, D, ... 를 다음과 같이 표현할 수 있다.
A = a*M + r, B = b*M + r, C = c*M + r, D = d*M + r, ... (M과 r은 모두 같고 M의 계수만 달라진다)
나는 처음에 여기서 r이 1~MIN(A~...)일 경우를 다 따로 생각을 해버렸기 때문에 시간 초과가 났었다. 그런데 M을 최대 공약수로 두어 찾고, 그의 약수들을 따로 카운트한다면 r이 얼마이든 상관 없어진다. 더 자세히 적어보겠다.
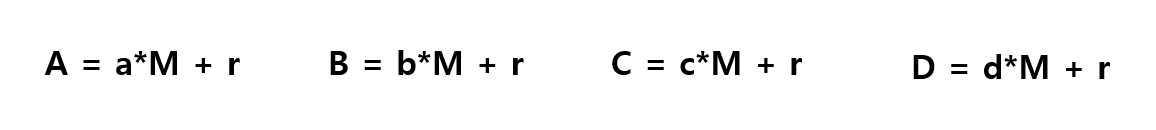
위에서 잠깐 언급한 것처럼 주어진 수(A, B, C, D)를 우리가 구하고자 하는 공약수 M과 특정 나머지 값 r을 사용해 수식화한 모습이다.
여기서 M을 따로 빼내기 위해 이웃한 수식의 양변을 서로 빼보자.
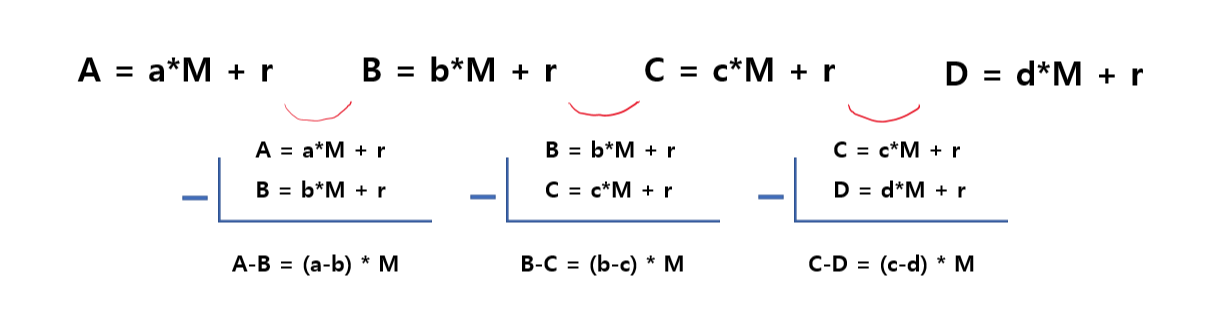
결과는 이렇게 된다. 이웃한 A=()와 B=()을 빼고, B=()와 C=(), C=()와 D=()를 빼었다. 그러면 공통된 나머지 r은 그 수가 무엇이었던 간에 삭제가 되고, 주어진 수와 M만이 남게 된다. 이것이 r의 경우를 일일이 생각했던게 패착이 되었던 이유다. 생각할 필요가 없다.
그럼 여기에서 보기 쉽게 A-B, B-C, C-D를 각각 X, Y, Z로 치환해보자.
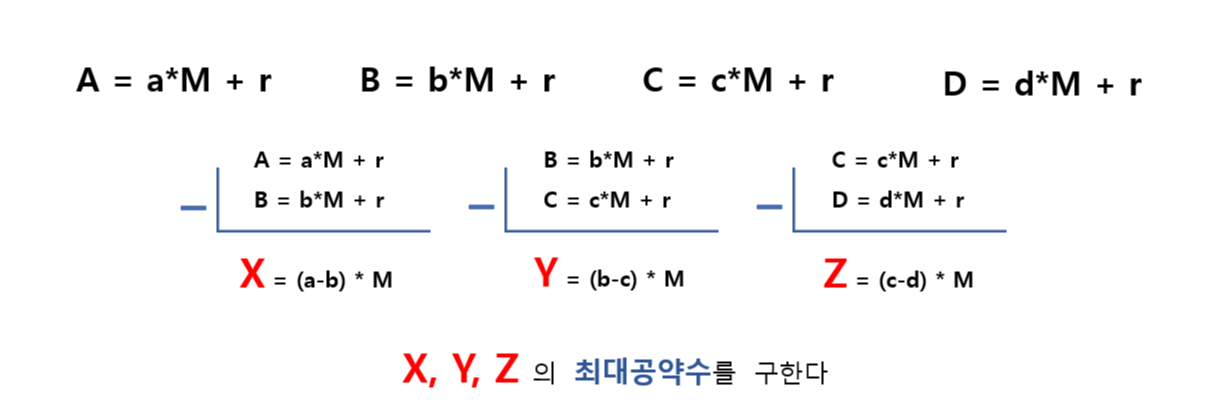
이제 우리가 찾고자 하는 나누는 수 M을 어떻게 구할 수 있을지 실마리가 보인다. 바로 X, Y, Z의 최대공약수를 구하는 것이다.
N가지 수의 최대공약수(gcd)를 구하기 위해서는 총 N-1번 gcd 구하기 과정을 거치면 된다. 먼저, 맨 앞 두 수의 gcd를 구한 뒤, 그 gcd와 다음 세번째 수의 gcd를, 다시 그 gcd와 마지막 수의 gcd까지 반복하면 된다.
그렇게 구한 gcd의 약수를 출력하면 된다. 단, M은 1보다 큰 수이니 1을 포함하지 않는 데 주의한다.
// 1. 주어진 수를 정렬
arr[i=0~N-1] = br.read();
Arrays.sort(arr)
// 2. 이웃한 수끼리 뺄셈한 결과끼리 gcd를 구함
gcd = arr[i]-arr[i-1]
for(i=1~N-1){
gcd = GCD(gcd, arr[i]-arr[i-1])
}
// 3. 구한 gcd(==M)의 약수 출력 (단, 1은 제외)
for(i=2~gcd){
if(i가 gcd 약수면)
sout(i)
}
최종 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.PriorityQueue;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] nums = new int[N];
for(int i=0; i<N; i++)
nums[i] = Integer.parseInt(br.readLine());
// 정렬
Arrays.sort(nums);
// 이웃한 수의 차이끼리의 최대공약수(GCD)를 구한다
int gcd = nums[1]-nums[0];
for (int i = 2; i < N; i++) {
gcd = GCD(gcd, nums[i]-nums[i-1]);
}
StringBuilder sb = new StringBuilder();
PriorityQueue pq = new PriorityQueue();
// 구한 GCD의 약수를 pq에 넣는다
for(int i=2; i<=Math.sqrt(gcd); i++){
// 제곱근은 따로 넣음
if(i*i == gcd)
pq.add(i);
else if(gcd%i == 0) {
pq.add(i);
pq.add(gcd / i);
}
}
// GCD도 넣음
pq.add(gcd);
while (!pq.isEmpty())
sb.append(pq.poll()).append(' ');
System.out.println(sb);
}
// a: 나뉠 수(B), b: 나눌 수(A%B)
static int GCD(int a, int b){
int tmp;
while(b!=0){
tmp = a % b;
a = b;
b = tmp;
}
return a;
}
}느낀점
- 기초의 중요성
- 사실 기업 코테에는 잘 안나오지 않을 것 같다..