2022 KAKAO BLIND RECRUITMENT 파괴되지 않은 건물
링크 : https://programmers.co.kr/learn/courses/30/lessons/92344
사용 언어 : JAVA
문제 설명
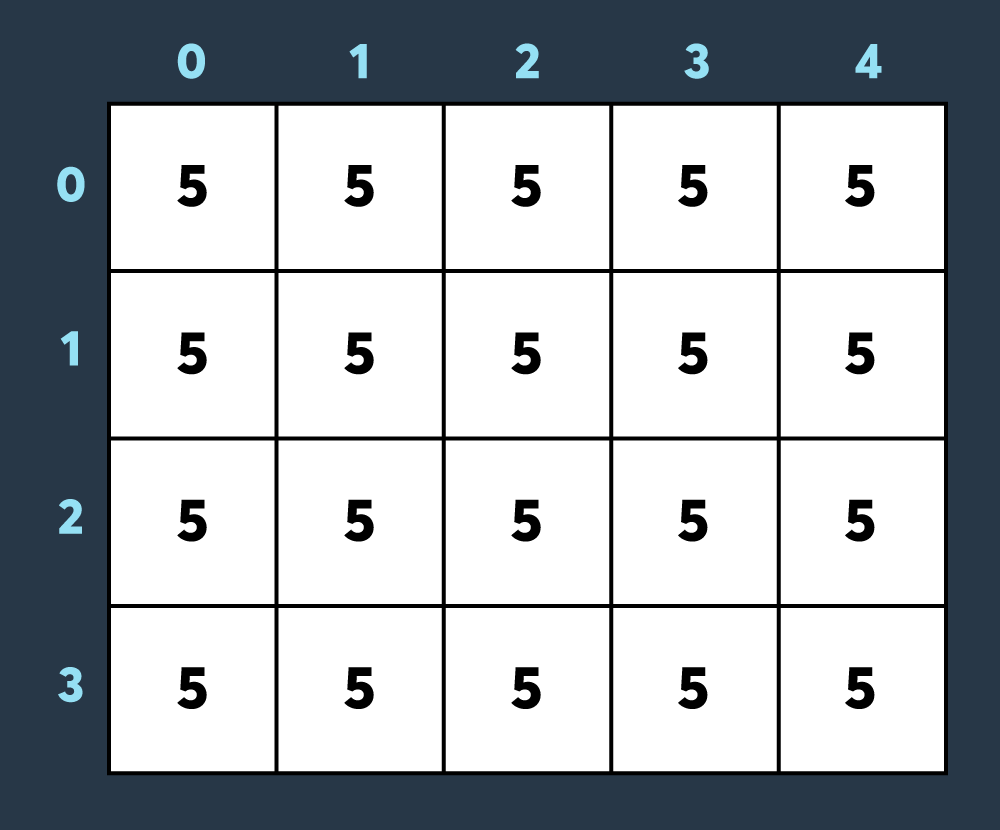
N x M 크기의 행렬 모양의 게임 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있다.
적은 이 건물들을 공격하여 파괴하려고 하고, 반대로 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려 한다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴된다.
적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 구하라.
첫 번째 스킬: 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮춤
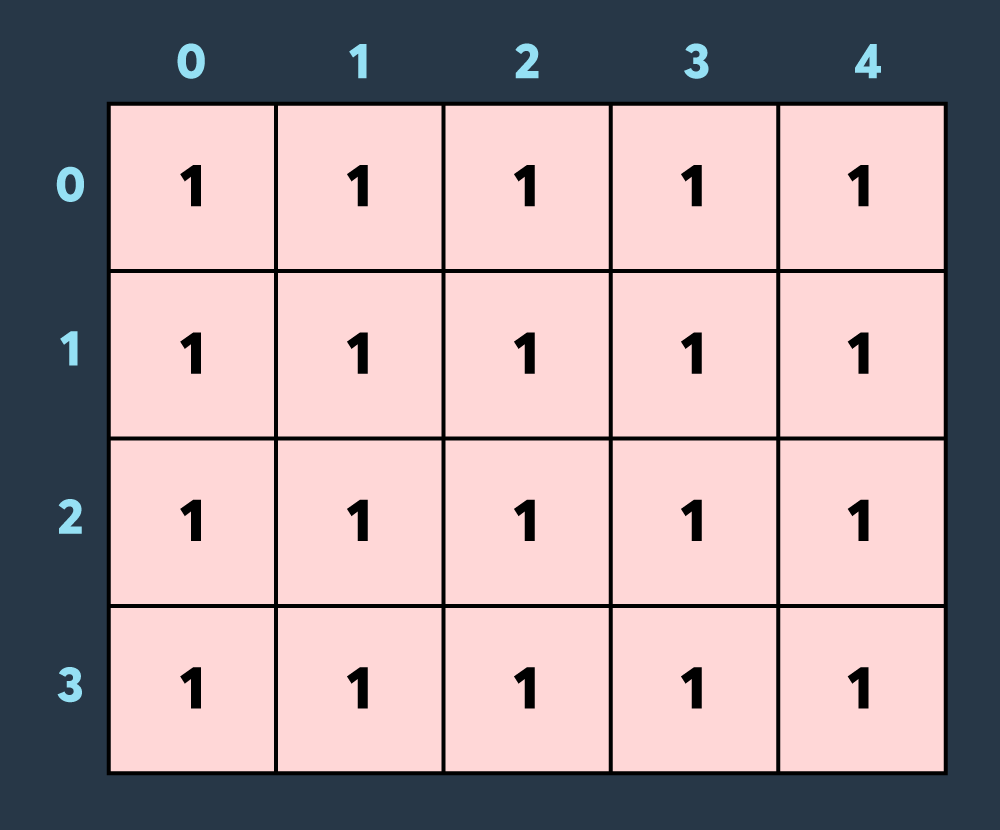
두 번째 스킬: 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮춤
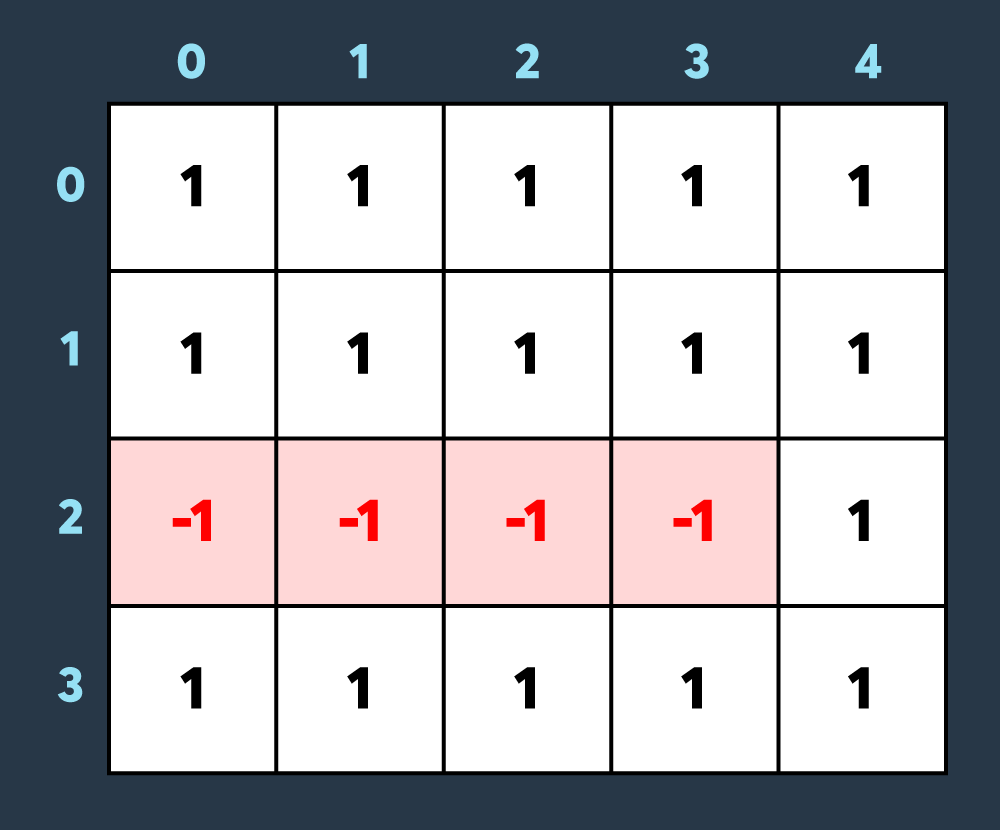
세 번째 스킬: 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높임. 결과로 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 된다.
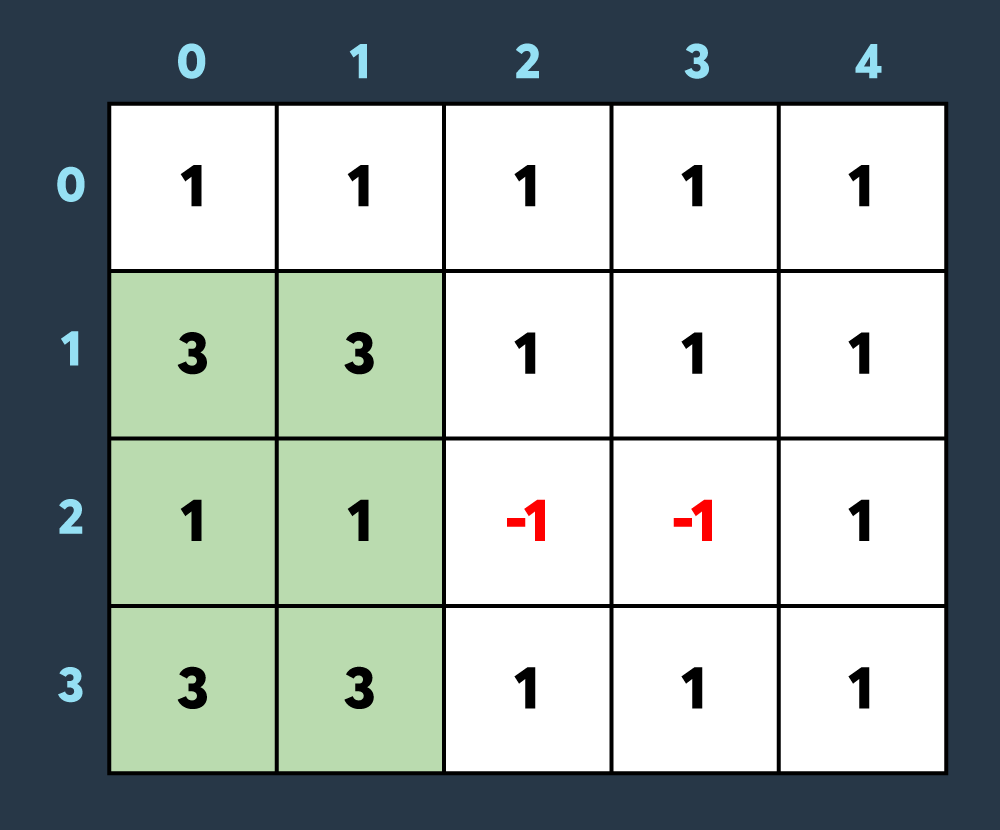
마지막 스킬: 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮춤 -> 8개의 건물이 더 파괴. 총 10개의 건물이 파괴된 상태가 된다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의)
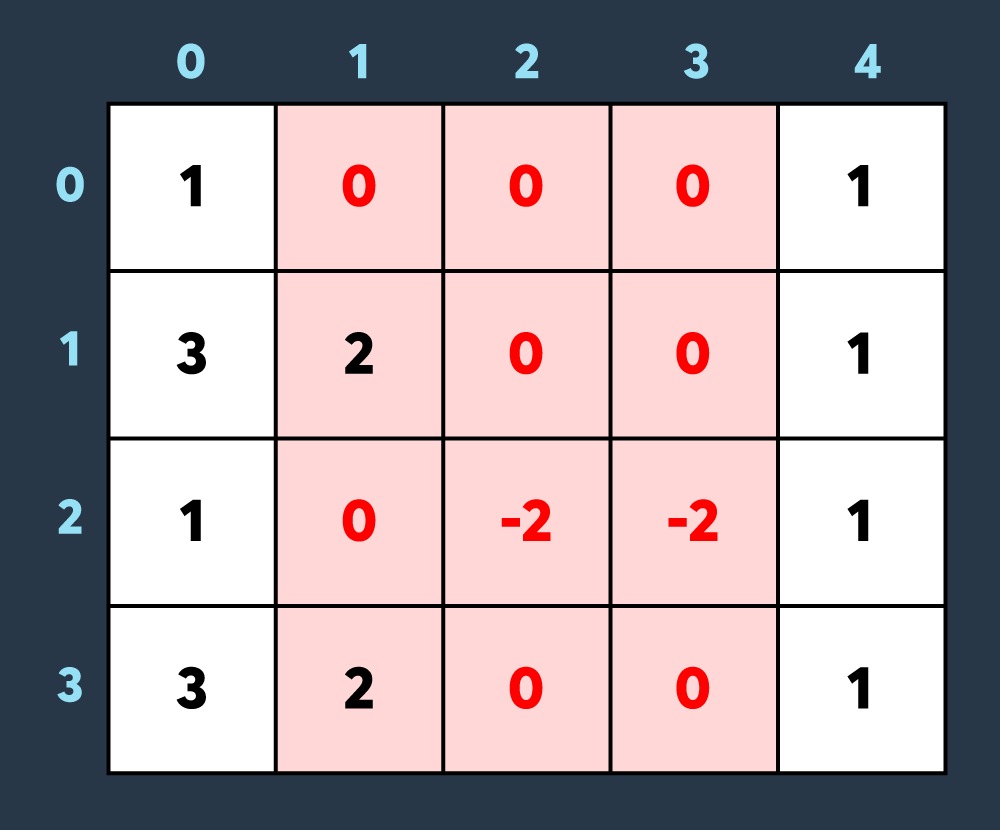
최종적으로 총 10개의 건물이 파괴되지 않은 상태로 남는다.
solution 함수 매개 변수
- int[][] board: 건물의 내구도를 나타내는 2차원 정수 배열
- int[][] skill: 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열, [type, r1, c1, r2, c2, degree]
- type = 1 or 2, 각각 적의 공격과 아군의 회복 스킬을 의미
- (r1, c1) ~ (r2, c2) 직사각형 범위에 degree 만큼 내구도를 낮추거나 높임
solution 함수 반환
- 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수
풀이
우선 이 문제는 누적합의 개념을 알아야 풀 수 있는 문제이다.
누적합이란?
구간에 나열된 수의 누적된 합을 의미한다.
1차원에서의 누적합

예를 들어 다음과 같은 나열된 수들이 있다고 할 때, 전체 구간의 누적합은 3+5+8+9+3+2+4+1+7+6 이 된다. 그냥 배열의 모든 인덱스를 참조하여 새로운 변수에 합한 결과값을 저장하는 것이다. 이 방식을 코드로 나타내면 아래와 같다.
int sum = 0;
for(int e: array){
sum += e;
}N개의 구간 에 대해 구간의 길이가 M인 구간합을 구하는 경우 이 방식의 시간 복잡도는 O(NM)이 된다.
이게 무슨말이냐,

위의 그림처럼 3개의 구간의 구간합을 구하고자 한다면
int sum1 = 0; // blue
int sum2 = 0; // orange
int sum3 = 0; // green
// Cumulative sum of blue area
for(int b=b1; b<b2+1; b++){
sum1 += array[b];
}
// Cumulative sum of orange area
for(int o=o1; o<o2+1; o++){
sum2 += array[o];
}
// Cumulative sum of green area
for(int g=g1; g<g2+1; g++){
sum3 += array[g];
}위와 같이 각각의 구간에 대한 구간합을 따로 구해야 하므로, 더하기 연산을 총 N*M 회 하게 되는 것이다.(위의 예제에서는 3*5회)
우리 문제에 이 방식을 적용한다면 모든 skill에 대해서 skill의 직사각형 범위 하나하나에 degree를 더하고 빼는 것이 된다. 하지만 효율성 문제이니만큼 변수 범위가 O(NM) 알고리즘으로 풀 수 없게 주어진다. 때문에 우리는 다른 방식을 고민해봐야 한다.
만약 새로운 변수 sum의 사용 없이 배열 내에서만 계산한다면 다음과 같을 것이다.
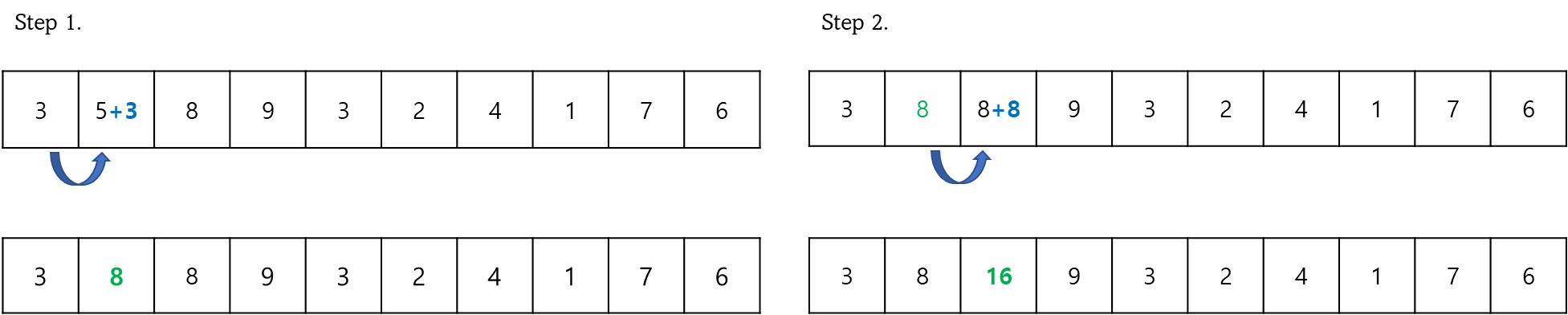

위의 과정을 끝까지 반복하면 이렇게 맨 마지막 인덱스에 누적합이 저장된다.

그럼 이 방식을 기억하고 다음 문제를 생각해보자.

파란 영역에는 5를, 노란 영역에는 -7을, 녹색 영역에는 3을 더해야 한다. 한번의 누적 합 계산을 통해 각 인덱스에 얼마가 저장되어야 하는지 알 수 있을까?
각 영역의 시작과 끝+1 인덱스에 아래처럼 마킹하고 누적합을 계산하면 각 영역의 합이 나온다.
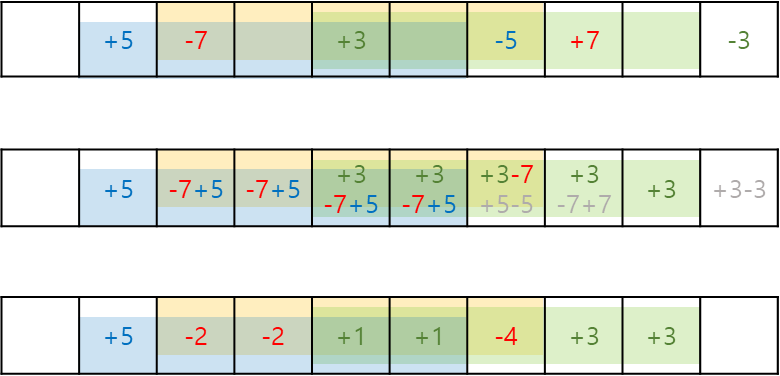
2차원에서의 누적합
이 방식을 2차원에서 생각한 것이 '파괴되지 않은 건물' 문제이다.
2차원에서 이 방식을 적용하려면 두 단계로 나뉜다. 우선 가로로 누적합을 구한 뒤, 세로로 각 열에 저장된 값의 누적합을 구한다.
1. 가로 누적합을 구한다
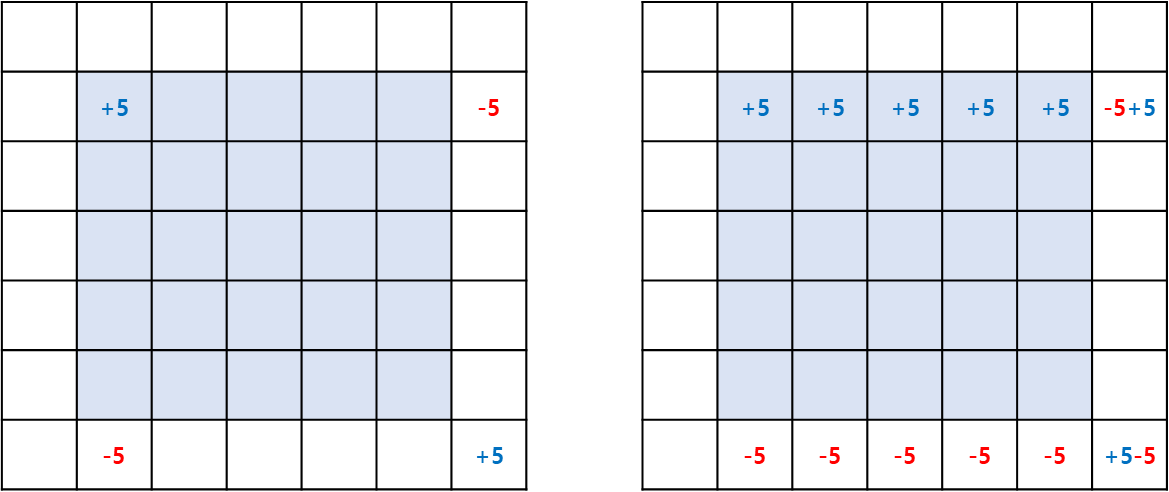
여기서 주의할 점은
+ -
- +
형식으로 마킹해야 한다는 것이다.
2. 세로 누적합을 구한다

원하는 2차원 범위에 degree만큼 더하거나 뺄 수 있게 된다.
N개의 구간 에 대해 구간의 길이가 M인 구간합을 구하는 경우 이 방식의 시간 복잡도는 O(N+M)이 된다.
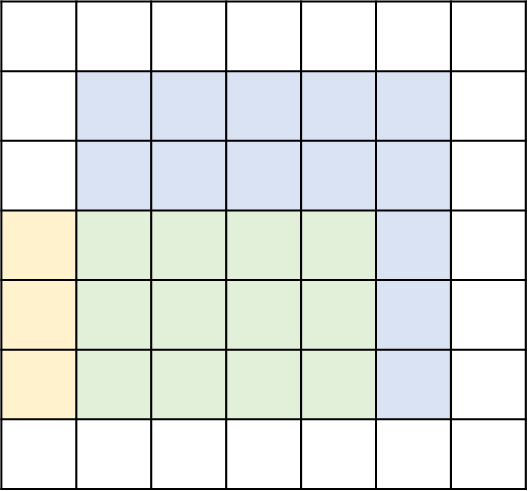
파란 영역에는 5를 더하고, 노란 부분에는 3을 더한다고 생각해 보자. (파란색과 노란색이 겹치는 영역은 녹색으로 표현하였다 -> 누적합이 8이 되어야 함)
1. 가로 누적합을 구한다
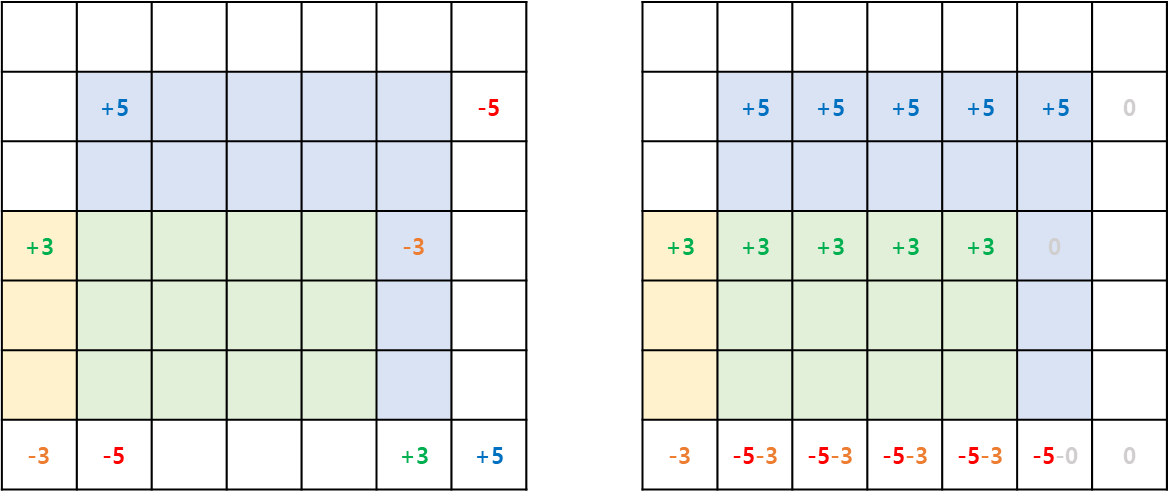
2. 세로 누적합을 구한다

최종 코드
class Solution {
public int solution(int[][] board, int[][] skill){
int answer = 0;
int R = board.length;
int C = board[0].length;
int[][] mark = new int[R+1][C+1];
// skill 포인트 찍기 [type, r1, c1, r2, c2, degree]
for(int[] s: skill) {
if(s[0]==2) {
mark[s[1]][s[2]] += s[5];
mark[s[1]][s[4]+1] -= s[5];
mark[s[3]+1][s[2]] -= s[5];
mark[s[3]+1][s[4]+1] += s[5];
} else {
mark[s[1]][s[2]] -= s[5];
mark[s[1]][s[4]+1] += s[5];
mark[s[3]+1][s[2]] += s[5];
mark[s[3]+1][s[4]+1] -= s[5];
}
}
// 가로 누적합 구하기
for(int r=0; r<R+1; r++) {
for(int c=0; c<C; c++) {
mark[r][c+1] += mark[r][c];
}
}
// 세로 누적합 구하기
for(int c=0; c<C+1; c++) {
for(int r=0; r<R; r++) {
mark[r+1][c] += mark[r][c];
}
}
// 파괴되지 않은 건물 찾기
for(int r=0; r<R; r++) {
for(int c=0; c<C; c++) {
if(mark[r][c] + board[r][c] > 0) ++answer;
}
}
return answer;
}
}느낀점
- 누적합이 무엇인지, 어떻게 구현하는 건지 알게되었다.
