[알고리즘] LCS(Longest Common Substring), 최장 공통 부분 수열 구현

LCS(Longest Common Substring)

정의

최장 공통 부분 수열. 주어진 여러 개의 수열의 부분 수열이 되는 수열들 중에 가장 긴 것을 찾는 문제이다. 백준의 이 문제를 보면 어떤 것인지 이해할 수 있다. (LIS: Longest Increasing Subsequence와 비슷하지만 다른 문제다)

LCS는 항상 유일하지 않기 때문에 보통 길이를 묻는 문제가 나온다.

 

알고리즘

여러 문자열의 LCS를 효율적으로 구하기 위해서 DP가 사용된다.

두 문자열 사이의 LCS 길이를 저장하는 2차원 배열 LCS를 만들고, 아래와 같은 방식으로 배열을 채운다.

X, Y 문자열 앞에 0을 넣는 이유는, i=1 || j=1일 때 Xi-1, Yj-1 값을 참조해야 할 수도 있기 때문에 만들어두는 것이다.

 

아래의 간단한 예제를 보며 과정을 익혀보자.

 

 

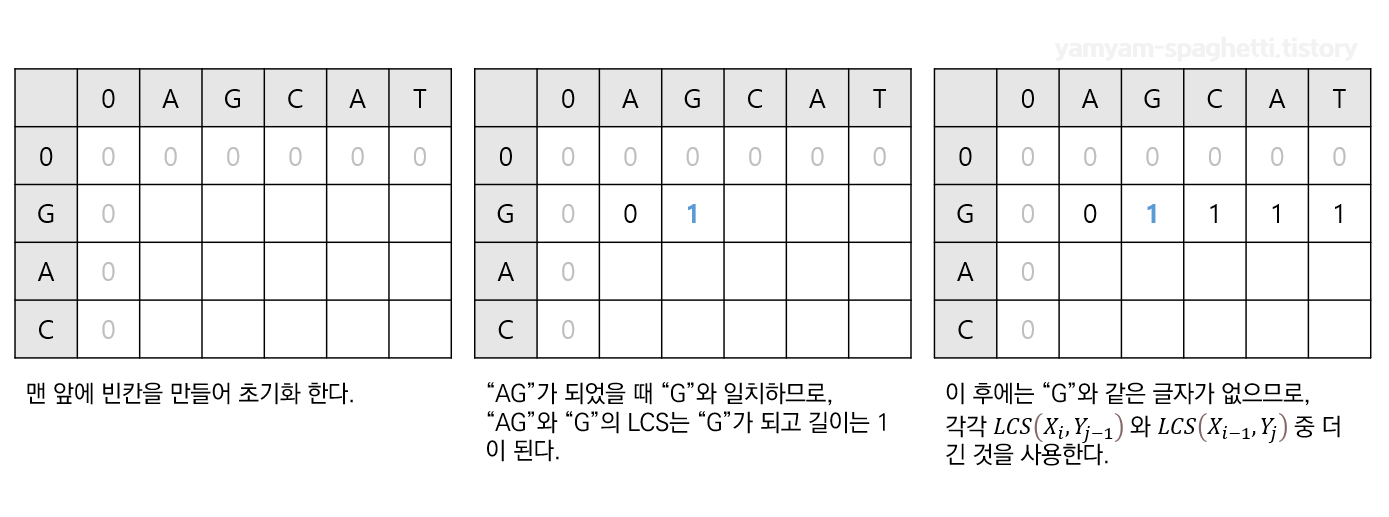
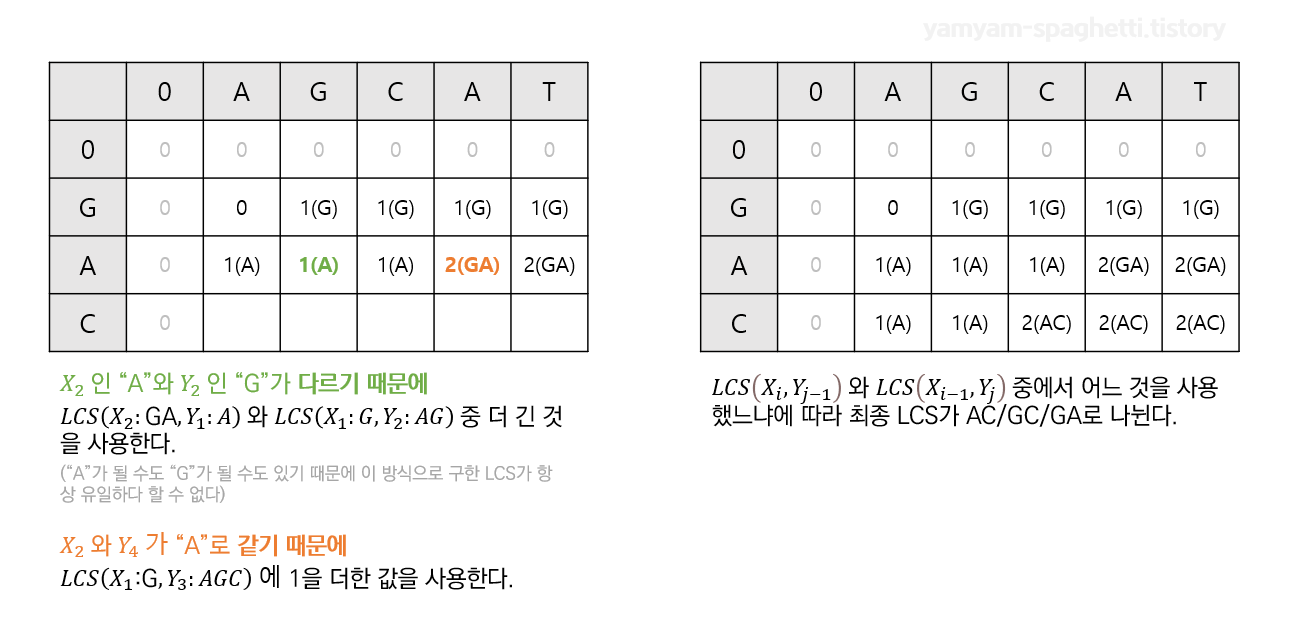
구현

길이 연산

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String X = " " + br.readLine();
        String Y = " " + br.readLine();

        int xl = X.length();
        int yl = Y.length();

        // LCS 길이 담는 배열
        int[][] LCS = new int[xl][yl];

        // init
        for(int i=0; i<xl; i++) {
        	LCS[i][0] = 0;
        }
        for(int i=0; i<yl; i++) {
        	LCS[0][i] = 0;
        }

        // 모든 LCS 계산
        for(int r=1; r<xl; r++) {
            for(int c=1; c<yl; c++) {
                if(X.charAt(r) == Y.charAt(c)) {
                	LCS[r][c] = LCS[r-1][c-1] + 1;
                } else {
                	LCS[r][c] = Math.max(LCS[r-1][c], LCS[r][c-1]);
                }
            }
        }

        System.out.println(LCS[xl-1][yl-1]);
    }
}

 

LCS 하나 찾기

public static String backTracking(int[][] LCS, char[] X, char[] Y, int i, int j) {
    if(i==0 || j==0) return "";

    if(X[i] == Y[j]) return backTracking(LCS, X, Y, i-1, j-1) + X[i];
    if(LCS[i][j-1] > LCS[i-1][j]) return backTracking(LCS, X, Y, i, j-1);
    return backTracking(LCS, X, Y, i-1, j);
}