문제
링크 : https://school.programmers.co.kr/learn/courses/30/lessons/12984
사용 언어 : JAVA


내 생각
초기 생각
// floor in [max_floor, 0]
func(money, floor) {
// 현재 floor를 기준으로 지형을 모두 메운다
// money1: floor까지 다 채우는 비용
money1 = fillFloor(floor);
MIN = Math.min(MIN, money);
// 현재 floor의 모든 지형을 삭제한다
// money2: floor를 다 삭제하는 비용
money2 = delFloor(floor);
// 현재 층을 다 밀고 아래 층을 기준으로 func 반복
func(money + money2, floor-1);
}대충 저런 구조였다. fillFloor()와 delFloor()가 각각 O(N^2)씩 걸리기 때문에 시간초과
개선
이래저래 시도해봤는데 못풀겠어서 결국 검색했고..ㅎ 나는 이분의 글을 참고하여 풀었다. (완전 동일하진 않음)
[프로그래머스] LV.4 지형 편집
XX 게임에서는 지형 편집 기능을 이용하여 플레이어가 직접 게임 속 지형을 수정할 수 있습니다. 이 게임에서는 1 x 1 x 1 크기의 정육면체 블록을 쌓아 게임 속 지형을 표현합니다. 이때, 블록이
velog.io
2차원 배열을 1차원으로 바꾸고 정렬을 하여 이전의 값을 활용할 수 있다는 아주 좋은 인사이트를 얻었다 ‼️
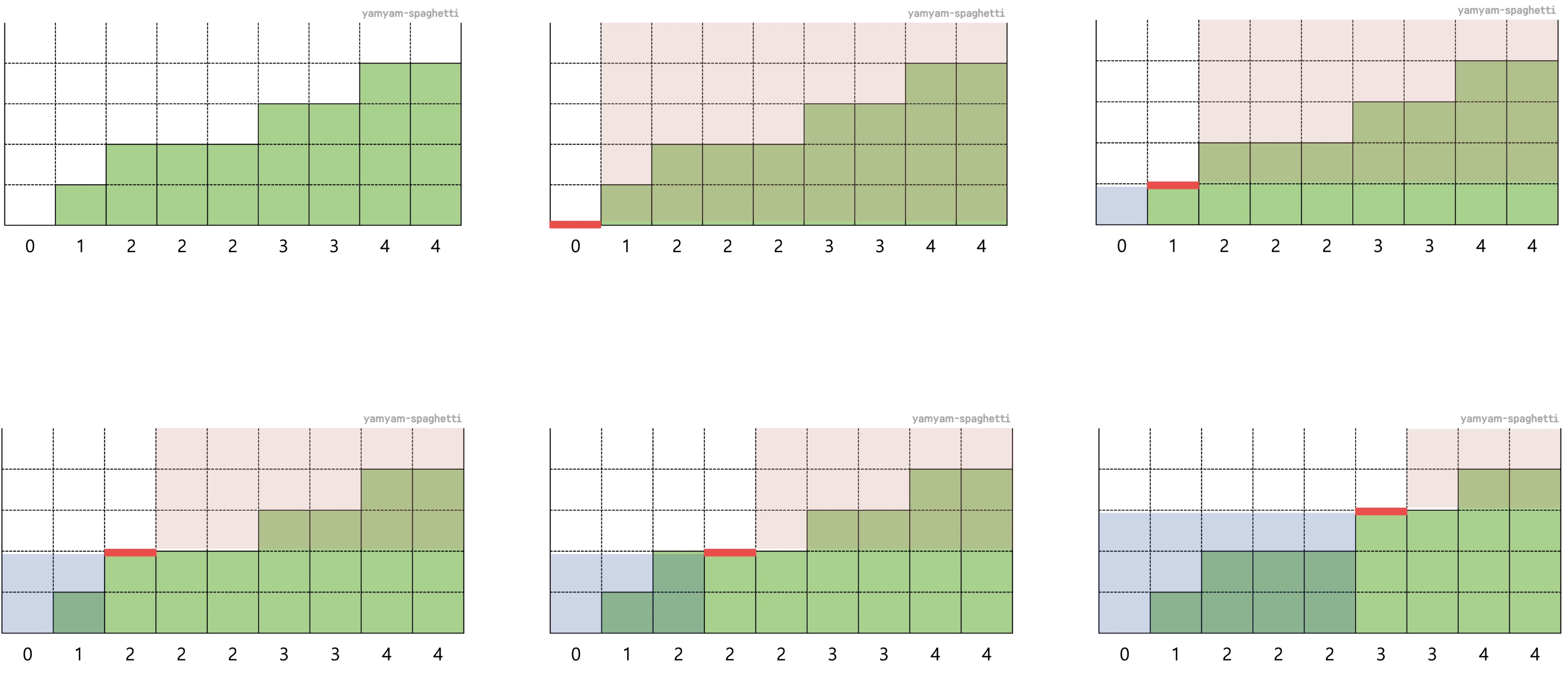
land[][] 배열을 1차원의 blocks[] 배열로 변경한 뒤 정렬을 하면 좌측 최상단 그림으로 표현할 수 있다.
blocks의 각 값을 기준 높이로 세워 추가 지형, 삭제 지형 개수를 생각해 보자. (이전 상태의 값을 재활용할 것이므로 이전의 추가/삭제 지형 개수를 저장할 길이 2짜리 prev[] 배열을 사용했다)
만약 기준 높이가 (blocks[i] - blocks[i-1])만큼 변경되면 (blocks[i] - blocks[i-1]) * N 에 해당하는 직사각형 범위를 아래처럼 나누어 prev에 반영하면 된다.
- 추가 [0, i)
- 삭제 [i, N)
과정을 천천히 보자.
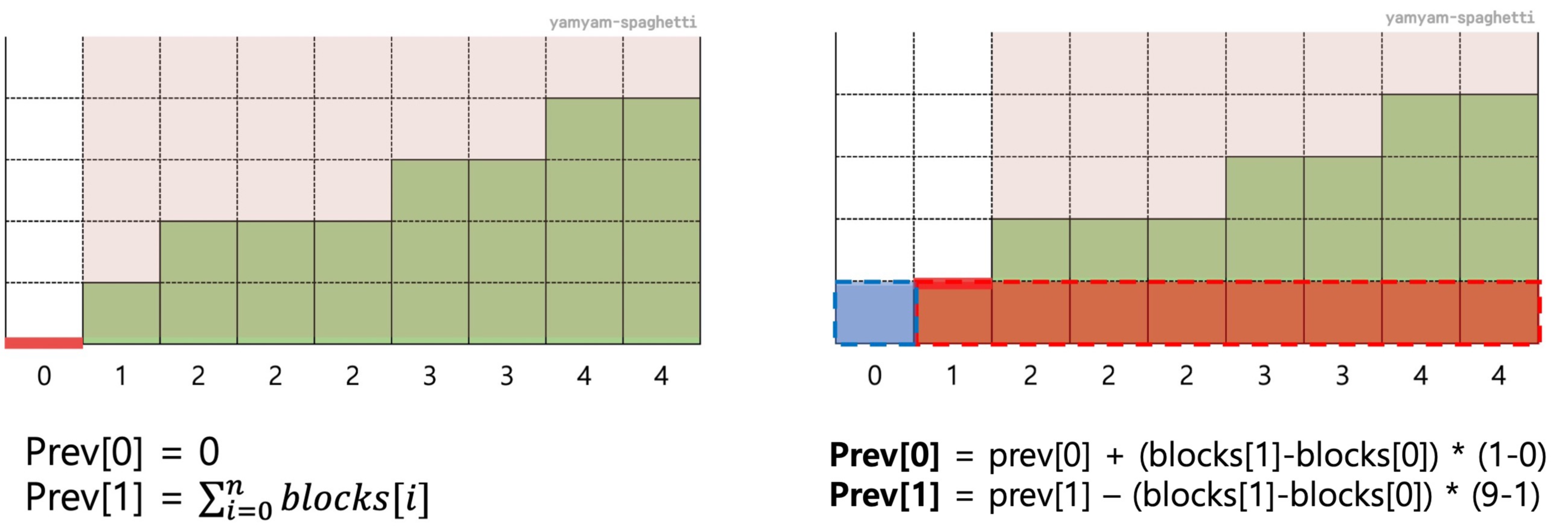
blocks[0] 기준
prev의 초기값은 높이가 0일때를 기준으로 맞췄다. 높이가 0이므로 추가 지형은 0, 삭제 지형은 현재 존재하는 모든 땅이 된다. (이 경우에는 blocks[0]의 값이 0이기 때문에 초기화 값을 그대로 가져다 썼다)
blocks[1] 기준
- prev[0] = 기존 prev[0] + 파란 점선 범위 (blocks[1]과 blocks[0]의 높이 차) * (맨 처음부터 1 이전까지의 너비)
- prev[1] = 기존 prev[1] - 빨간 점선 범위 (blocks[1]과 blocks[0]의 높이 차) * (1부터 맨 끝까지의 너비)
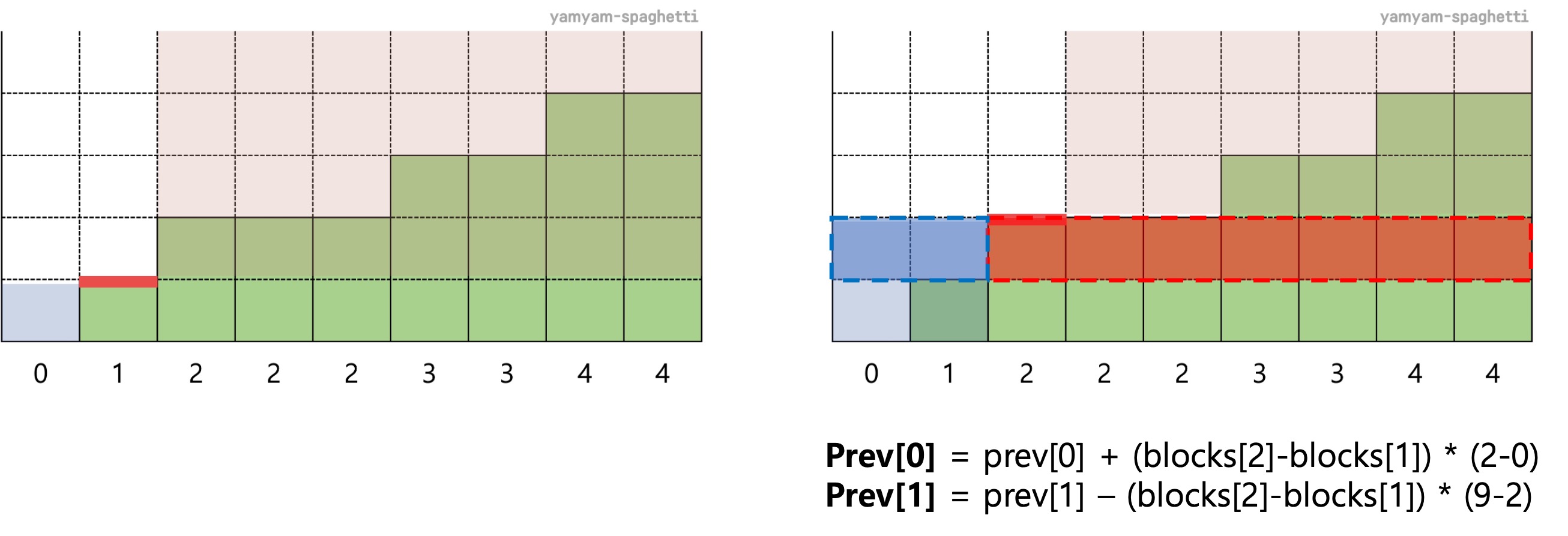
blocks[2] 기준
- prev[0] = 기존 prev[0] + 파란 점선 범위 (blocks[2]과 blocks[1]의 높이 차) * (맨 처음부터 2 이전까지의 너비)
- prev[1] = 기존 prev[1] - 빨간 점선 범위 (blocks[2]과 blocks[1]의 높이 차) * (2부터 맨 끝까지의 너비)
저 방법이 반복되면 이렇게 정리할 수 있다.
- prev[0] = prev[0] + (blocks[i] - blocks[i - 1]) * i
- prev[1] = prev[1] - (blocks[i] - blocks[i - 1]) * (N - i)
모든 blocks를 기준으로 prev 값을 구하고, 구한 prev 값으로 지형 추가/삭제 비용을 계산해 최솟값을 갱신하면 된다.
최종 코드
public long solution(int[][] land, int P, int Q) {
int N = land.length * land.length;
long[] prev = new long[2];
// land를 1차원 배열 blocks로 변경
long[] blocks = new long[N];
for(int i=0, n=land.length; i<N; i++) {
blocks[i] = land[i / n][i % n];
}
Arrays.sort(blocks);
long sum = 0;
for(int i=0; i<N; i++) {
sum += blocks[i];
}
// 0번째 인덱스를 기준으로 prev 초기화
// prev[0]은 더 추가할 게 없으므로 0, prev[1]은 모든 칸에서 blocks[0] 높이 만큼을 제외한다.
prev[1] = sum - (blocks[0] * N);
// 모두 제외해서 높이가 blocks[0]이 될 때의 비용으로 초기화
long MIN = prev[1] * Q;
// blocks[1~N]의 높이를 기준으로 지형을 추가/삭제
for (int i = 1; i < N; i++) {
if (blocks[i] == blocks[i - 1]) continue;
prev[0] += (blocks[i] - blocks[i - 1]) * i;
prev[1] -= (blocks[i] - blocks[i - 1]) * (N - i);
// 만약 최소 비용보다 더 나왔다면 더 이상 탐색하지 않음
if (MIN < prev[0] * P + prev[1] * Q) break;
// 최소 비용 갱신
MIN = prev[0] * P + prev[1] * Q;
}
return MIN;
}느낀점
- 처음부터 시간 복잡도를 계산해서 제대로 푸는 연습을 해야겠다.
문제
링크 : https://school.programmers.co.kr/learn/courses/30/lessons/12984
사용 언어 : JAVA


내 생각
초기 생각
// floor in [max_floor, 0]
func(money, floor) {
// 현재 floor를 기준으로 지형을 모두 메운다
// money1: floor까지 다 채우는 비용
money1 = fillFloor(floor);
MIN = Math.min(MIN, money);
// 현재 floor의 모든 지형을 삭제한다
// money2: floor를 다 삭제하는 비용
money2 = delFloor(floor);
// 현재 층을 다 밀고 아래 층을 기준으로 func 반복
func(money + money2, floor-1);
}대충 저런 구조였다. fillFloor()와 delFloor()가 각각 O(N^2)씩 걸리기 때문에 시간초과
개선
이래저래 시도해봤는데 못풀겠어서 결국 검색했고..ㅎ 나는 이분의 글을 참고하여 풀었다. (완전 동일하진 않음)
[프로그래머스] LV.4 지형 편집
XX 게임에서는 지형 편집 기능을 이용하여 플레이어가 직접 게임 속 지형을 수정할 수 있습니다. 이 게임에서는 1 x 1 x 1 크기의 정육면체 블록을 쌓아 게임 속 지형을 표현합니다. 이때, 블록이
velog.io
2차원 배열을 1차원으로 바꾸고 정렬을 하여 이전의 값을 활용할 수 있다는 아주 좋은 인사이트를 얻었다 ‼️

land[][] 배열을 1차원의 blocks[] 배열로 변경한 뒤 정렬을 하면 좌측 최상단 그림으로 표현할 수 있다.
blocks의 각 값을 기준 높이로 세워 추가 지형, 삭제 지형 개수를 생각해 보자. (이전 상태의 값을 재활용할 것이므로 이전의 추가/삭제 지형 개수를 저장할 길이 2짜리 prev[] 배열을 사용했다)
만약 기준 높이가 (blocks[i] - blocks[i-1])만큼 변경되면 (blocks[i] - blocks[i-1]) * N 에 해당하는 직사각형 범위를 아래처럼 나누어 prev에 반영하면 된다.
- 추가 [0, i)
- 삭제 [i, N)
과정을 천천히 보자.

blocks[0] 기준
prev의 초기값은 높이가 0일때를 기준으로 맞췄다. 높이가 0이므로 추가 지형은 0, 삭제 지형은 현재 존재하는 모든 땅이 된다. (이 경우에는 blocks[0]의 값이 0이기 때문에 초기화 값을 그대로 가져다 썼다)
blocks[1] 기준
- prev[0] = 기존 prev[0] + 파란 점선 범위 (blocks[1]과 blocks[0]의 높이 차) * (맨 처음부터 1 이전까지의 너비)
- prev[1] = 기존 prev[1] - 빨간 점선 범위 (blocks[1]과 blocks[0]의 높이 차) * (1부터 맨 끝까지의 너비)

blocks[2] 기준
- prev[0] = 기존 prev[0] + 파란 점선 범위 (blocks[2]과 blocks[1]의 높이 차) * (맨 처음부터 2 이전까지의 너비)
- prev[1] = 기존 prev[1] - 빨간 점선 범위 (blocks[2]과 blocks[1]의 높이 차) * (2부터 맨 끝까지의 너비)
저 방법이 반복되면 이렇게 정리할 수 있다.
- prev[0] = prev[0] + (blocks[i] - blocks[i - 1]) * i
- prev[1] = prev[1] - (blocks[i] - blocks[i - 1]) * (N - i)
모든 blocks를 기준으로 prev 값을 구하고, 구한 prev 값으로 지형 추가/삭제 비용을 계산해 최솟값을 갱신하면 된다.
최종 코드
public long solution(int[][] land, int P, int Q) {
int N = land.length * land.length;
long[] prev = new long[2];
// land를 1차원 배열 blocks로 변경
long[] blocks = new long[N];
for(int i=0, n=land.length; i<N; i++) {
blocks[i] = land[i / n][i % n];
}
Arrays.sort(blocks);
long sum = 0;
for(int i=0; i<N; i++) {
sum += blocks[i];
}
// 0번째 인덱스를 기준으로 prev 초기화
// prev[0]은 더 추가할 게 없으므로 0, prev[1]은 모든 칸에서 blocks[0] 높이 만큼을 제외한다.
prev[1] = sum - (blocks[0] * N);
// 모두 제외해서 높이가 blocks[0]이 될 때의 비용으로 초기화
long MIN = prev[1] * Q;
// blocks[1~N]의 높이를 기준으로 지형을 추가/삭제
for (int i = 1; i < N; i++) {
if (blocks[i] == blocks[i - 1]) continue;
prev[0] += (blocks[i] - blocks[i - 1]) * i;
prev[1] -= (blocks[i] - blocks[i - 1]) * (N - i);
// 만약 최소 비용보다 더 나왔다면 더 이상 탐색하지 않음
if (MIN < prev[0] * P + prev[1] * Q) break;
// 최소 비용 갱신
MIN = prev[0] * P + prev[1] * Q;
}
return MIN;
}느낀점
- 처음부터 시간 복잡도를 계산해서 제대로 푸는 연습을 해야겠다.
